Imagine you’re the manager of a made-up team we’ll call the San Francisco Dodgers, because I’m not very creative. It’s game seven of the World Series, and, for whatever reason, your pitching staff is so loaded that you have both Clayton Kershaw and Madison Bumgarner available to throw on full rest. Who do you start? And yes, it’s against the spirit of the question to say, “It doesn’t matter. I would pitch both for four innings, avoid the third time through the order penalty and hand the ball to my closer in the ninth.’”
That’s the question that sparked what has become an ongoing debate among my friends and I. It’s a silly argument to have in the sense that it revolves around how to optimize a hypothetical team’s chances of winning a hypothetical game seven of a hypothetical World Series. But it’s not so silly in an important way: Your choice of pitcher reveals how you grapple with small, noisy statistical samples that seem to contradict mountains of other evidence.
I’m, of course, alluding to the apparent divide between both Kershaw and Bumgarner’s regular season versus postseason stats. The conventional answer to the question of who to start in a game seven is Bumgarner for one simple reason: In the playoffs, Bumgarner’s numbers, measured by traditional statistics, suggest that he has performed substantially better than one would expect given his regular season output, while Kershaw has performed substantially worse. I don’t think anyone would dispute that Kershaw has been the superior regular season pitcher, but Bumgarner’s heroic postseason history seems to weigh heavily in people’s minds.
But is it the case that Kershaw typically struggles against playoff teams while Bumgarner excels? Aggregating both pitchers’ career regular season numbers against teams that went on to reach the postseason shows that no such differential exists. Excluding their rookie seasons — 2011-2017 for Bumgarner and 2009-2017 for Kershaw — Bumgarner has posted a 2.95 ERA against playoff teams compared to a 3.02 overall ERA, while Kershaw has registered a 2.25 ERA against playoffs teams and an identical 2.25 overall ERA.
The argument for starting Bumgarner in game seven must then rely on the idea that there’s something different about the postseason that brings out the best in him and the worst in Kershaw. I don’t deny that this might be the case for certain players. But given the sample sizes, how can you possibly know which ace is the better playoff pitcher?
For some, the answer is easy. “Just look at Bumgarner’s postseason ERA, it’s almost a full run lower than his regular season ERA! Kershaw’s is nearly two runs higher,” they might say.
The problem with putting so much emphasis on postseason ERA is that you’re relying on a tiny, volatile sample to determine how a pitcher will likely perform in the playoffs going forward. Kershaw has thrown just 122 playoff innings, and Bumgarner only 102 1/3. With so few observations, ERA is relatively meaningless — baseball is notoriously random, and it’s easy for a pitcher’s ERA to get hopelessly skewed over short stretches.
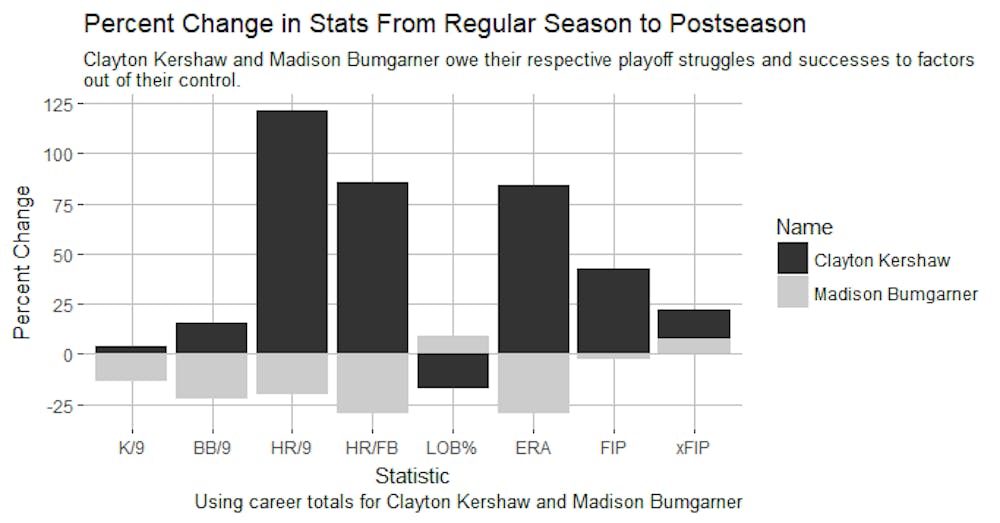
Consider the graphic attached, which shows the percent change in Kershaw and Bumgarner’s different statistical indicators from the regular season to the postseason.
Keep in mind while looking at the chart that, except for the strikeout per-nine and left on base percentage columns, positive changes are not good. Take the ERA column, for instance. Kershaw has seen his ERA rise by 84 percent in the playoffs compared to the regular season. That’s very bad.
Without getting too much into the weeds, the graphic shows that Bumgarner owes his playoff success — and Kershaw his playoff struggles — to factors that sabermetricians have identified as largely out of a pitcher’s control.
For example, the biggest difference between postseason Kershaw and regular season Kershaw can be seen in the home runs per nine innings column. In the playoffs, Kershaw has given up 122 percent more homers per nine innings than in the regular season, while Bumgarner has surrendered 20 percent fewer long balls. But those figures are driven in large part by each pitcher’s abnormal home run per flyball rates, a statistic far more reflective of random luck than pitcher skill in the short term. Balls lifted in the air against Kershaw in October have turned into home runs 86 percent more often compared to 30 percent less often for Bumgarner.
Bumgarner has also benefited from an artificially low batting average on balls in play, another statistic prone to wild short run fluctuation. It’s not pictured in the graphic, but batters are hitting just .236 on balls in play against Bumgarner in the playoffs, down from .284 in the regular season.
To combat that sort of randomness, researchers developed statistics that only include factors pitchers can control — think walk percentage, strikeout percentage and groundball percentage — to estimate a hurler’s ability to prevent runs. Those statistics are represented in the chart as the FIP and xFIP columns, the difference being that FIP penalizes pitchers for every home run allowed, while xFIP estimates the number of homers a pitcher “should have” given up assuming a league average HR/FB rate.
Sure enough, even though he has declined in the playoffs more than Bumgarner relative to his regular season baseline, Kershaw actually owns the better postseason xFIP, outpacing Bumgarner 3.34 to 3.60.
After a little more than 100 postseason innings for each ace, we’re left with Bumgarner, who has gotten better results due to what appears to be favorable random variation, and Kershaw, who has been more effective accounting only for the elements of the game in the pitcher’s control.
So which pitcher has been better in the postseason? I have no idea. As I’ve tried to illustrate, there’s evidence Kershaw has been the superior playoff pitcher, but at only 122 and 102 1/3 innings apiece, the error bars are just too wide.
But which pitcher am I starting in game seven? Give me Kershaw, the guy who over 1,935 regular season innings owns the lowest era-adjusted ERA of any starting pitcher in history.
Sam Grigo ’18 can be reached at samuel_grigo@brown.edu. Please send responses to this opinion to letters@browndailyherald.com and other op-eds to opinions@browndailyherald.com.